同次座標と二次元図形の基本的な幾何変換の行列導出

同次座標#

“同次座標表示はコンピュータグラフィックスの重要な手段の一つであり、ベクトルと点を明確に区別できるだけでなく、アフィン（線形）幾何変換を行うのにも便利です。”—— F.S. Hill, JR。

引用の通り、同次座標の最大の特徴は、座標と ベクトル を区別できることです。

簡単に言えば、通常の直交座標系（またはデカルト座標系とも言えます）では、(x_A, y_A) は点 A を表すこともでき、ベクトル $\vec{oA}$ を表すこともできます。この曖昧な表現は、コンピュータに対して正確な抽象的な説明を行うには不利です。

同次座標は n 次元を n+1 次元に拡張することでこの問題を解決します。

2D デカルト座標の末尾に追加の変数 w を加えることで 2D 同次座標を形成できます。したがって、点 (X,Y) は同次座標では (x,y,w) となり、次のようになります。

X = x/w

Y = y/w

同次座標では

点 A を表すには、(x_A, y_A, 1) と表現します。
ベクトル $\vec {oA}$ を表すには、(x_A, y_A, 0) と表現します。

w=1、0 を x/w に代入してみると、1 が点（位置）を、0 がベクトル（方向）を表す理由が理解できます。

さらに、ベクトル加法などの操作も便利になります。

もちろん、ベクトルと点を表現するだけでなく、同次座標の導入は幾何変換（線形変換）の表現も便利にします。

例えば、同次座標を使用しない二次元平行移動は以下のようになります。

二次元図形の基本的な幾何変換#

二次元図形の変換は大きく以下の五つのカテゴリに分けられます —— 平行移動（Translate）、拡大縮小（Scale）、回転（Rotate）、反射（Reflect）、およびせん断（shear）。

1. 平行移動#

点 (x, y) から (x + dx, y + dy) への変換を表現します。

同次座標を導入すると、(x, y, 1) が (x + dx, y + dy, 1) に変形されます。

この時、線形変換をツールとして変換プロセスを表現でき、変換行列を導入すると、この問題は変換行列を求めることに変わります。

既知:

\begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} = \begin{pmatrix} x + dx \\ y + dy \\ 1 \end{pmatrix}

得られるのは

\begin{cases} ax + by + c = x + dx \\ dx + ey + f = y + dy \\ gx + hy + i = 1 \end{cases}

変換行列は次のようになります。

\begin{pmatrix} 1 & 0 & dx \\ 0 & 1 & dy \\ 0 & 0 & 1 \end{pmatrix}

したがって、数学的な観点からこの変換行列を使用して平行移動プロセスを表現できます。

2. 拡大縮小#

点 (x, y) から (sx*x, sy*y) への変換を表現します。sx と sy は定数です。

同次座標を導入すると、(x, y, 1) が (sx*x, sy*y, 1) に変形されます。

変換行列を導入します。

既知:

\begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} = \begin{pmatrix} sx * x \\ sy * y \\ 1 \end{pmatrix}

得られるのは

\begin{cases} ax + by + c = sx * x \\ dx + ey + f = sy * y \\ gx + hy + i = 1 \end{cases}

変換行列は次のようになります。

\begin{pmatrix} sx & 0 & 0 \\ 0 & sy & 0 \\ 0 & 0 & 1 \end{pmatrix}

3. 回転#

回転を説明するには単位円を導入する必要があります。

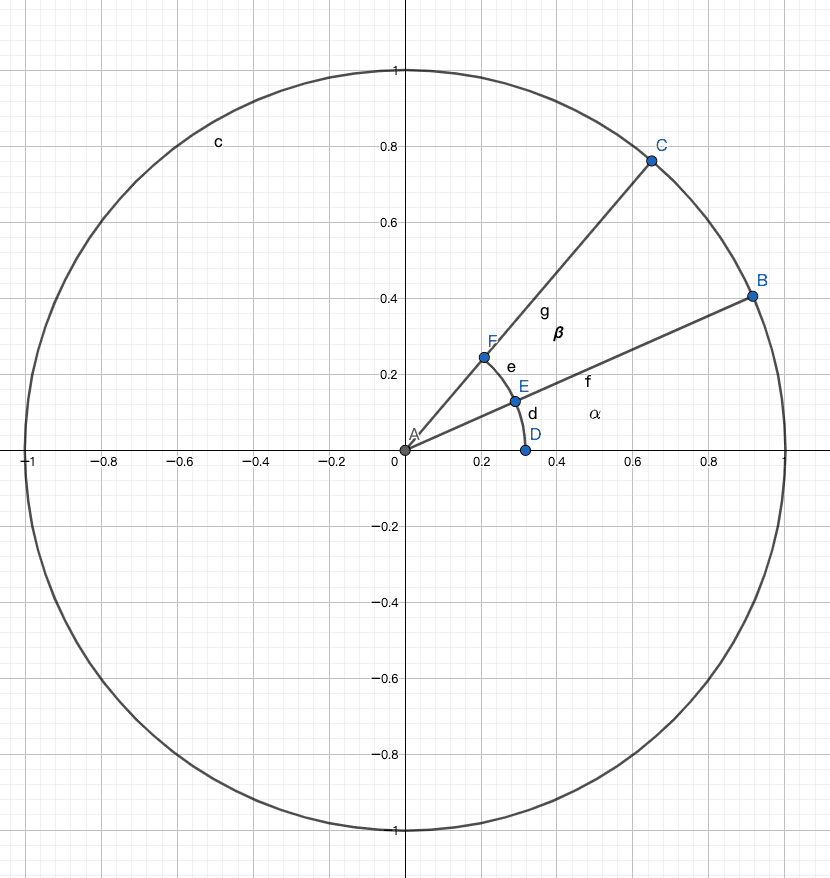
図のように、点 B が点 C に回転し、AB と X 軸の角度が α、AC と AB の角度が β です。

したがって、B 点の座標は (cosα, sinα)、C 点の座標は (cos (α + β), sin (α + β)) と表現できます。

C 点の座標を展開すると、C 点は (cosα cosβ - sinα sinβ, sinα cosβ + cosα sinβ) となります。

B 点の座標を (x, y) とし、C 点の座標は (x cosβ - y sinβ, y cosβ + x sinβ) となります。

同次座標を導入すると、(x, y, 1) が (x cosβ - y sinβ, y cosβ + x sinβ, 1) に変形されます。

変換行列を導入します。

既知:

\begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} = \begin{pmatrix} xcosβ - ysinβ \\ ycosβ + xsinβ \\ 1 \end{pmatrix}

得られるのは

\begin{cases} ax + by + c = xcosβ - ysinβ \\ dx + ey + f = ycosβ + xsinβ \\ gx + hy + i = 1 \end{cases}

変換行列は次のようになります。

\begin{pmatrix} cosβ & -sinβ & 0 \\ sinβ & cosβ & 0 \\ 0 & 0 & 1 \end{pmatrix}

4. 反射#

数学において、反射は物体をその鏡像に変換する写像です。平面図形を反射するには、「鏡」として直線（反射軸）が必要であり、三次元空間での反射には平面を鏡として使用します。

引用に基づくと、反射は X 軸に基づく反射と Y 軸に基づく反射に分けられますが、実際には中心反射（点反射）という概念も存在します。

X 軸に基づく反射#

点 (x, y) から点 (x, -y) への変換を表現します。

既知:

\begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} = \begin{pmatrix} x \\ -y \\ 1 \end{pmatrix}

得られるのは:

\begin{cases} ax + by + c = x \\ dx + ey + f = -y \\ gx + hy + i = 1 \end{cases}

変換行列は次のようになります:

\begin{pmatrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 1 \end{pmatrix}

Y 軸に基づく反射#

点 (x, y) から点 (-x, y) への変換を表現します。

既知:

\begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} = \begin{pmatrix} -x \\ y \\ 1 \end{pmatrix}

得られるのは:

\begin{cases} ax + by + c = -x \\ dx + ey + f = y \\ gx + hy + i = 1 \end{cases}

変換行列は次のようになります:

\begin{pmatrix} -1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}

点 (p, q) に基づく反射#

点 (x, y) から点 (2p-x, 2q-y) への変換を表現します。

既知:

\begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} = \begin{pmatrix} 2p-x \\ 2q-y \\ 1 \end{pmatrix}

得られるのは:

\begin{cases} ax + by + c = 2p-x \\ dx + ey + f = 2q-y \\ gx + hy + i = 1 \end{cases}

変換行列は次のようになります:

\begin{pmatrix} -1 & 0 & 2p \\ 0 & -1 & 2q \\ 0 & 0 & 1 \end{pmatrix}

5. せん断#

定義は図に見られる通りで、実際には図形がある方向に歪むようなものです。以下に推導過程を示します。α と β の範囲は [0, 90°) であることに注意してください。

Y 軸を依存軸とするせん断変換#

点 (x, y) から点 (x + y.tanα, y) への変換を表現します。

既知:

\begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} = \begin{pmatrix} x+y.tanα \\ y \\ 1 \end{pmatrix}

得られるのは:

\begin{cases} ax + by + c = x+y.tanα \\ dx + ey + f = y \\ gx + hy + i = 1 \end{cases}

変換行列は次のようになります:

\begin{pmatrix} 1 & tanα & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}

X 軸を依存軸とするせん断変換#

点 (x, y) から点 (x, y + x.tanβ) への変換を表現します。

既知:

\begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} = \begin{pmatrix} x \\ y + x.tanβ \\ 1 \end{pmatrix}

得られるのは:

\begin{cases} ax + by + c = x \\ dx + ey + f = y + x.tanβ \\ gx + hy + i = 1 \end{cases}

変換行列は次のようになります:

\begin{pmatrix} 1 & 0 & 0 \\ tanβ & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}