齐次坐标#
“齐次坐标表示是计算机图形学的重要手段之一，它既能够用来明确区分向量和点，同时也更易用于进行仿射（线性）几何变换。”—— F.S. Hill, JR。
正如引用中所说，齐次坐标最大的特点在于它的存在可以区分描述 坐标 与 向量
简单的来说，在普通的直角坐标系（或者说笛卡尔坐标系也行）中，(xA , yA ) 可以表示点 A，也可以用来表示向量 o A ⃗ \vec{oA} o A
而齐次坐标通过将 n 维提升到 n+1 维从而解决了这个问题。
我们可以在一个 2D 笛卡尔坐标末尾加上一个额外的变量 w 来形成 2D 齐次坐标，因此，一个点 (X,Y) 在齐次坐标里面变成了（x,y,w），并且有
X = x/w
Y = y/w
如在齐次坐标中
描述一个点 A，其表示为 (xA , yA , 1)
描述一个向量 $\vec {oA}$，其表示为 (xA , yA , 0)
试着将 w=1，0 带入 x/w，便可以理解为何 1 表示点（位置）、0 表示向量（方向）了。
除此之外也方便进行向量加法之类的操作
当然除了描述向量与点外，齐次坐标的引入也方便描述几何变换 (线性变换)。
比如如果不用齐次坐标表示的二维平移是下图这样的
二维图形基本几何变换#
二维图形变换大致分为以下五类 —— 平移（Translate）、缩放（Scale）、旋转（Rotate）、反射（Reflect）和错切（shear）
1. 平移#
描述从点 (x, y) 到 (x + dx, y+ dy)
引入齐次坐标，可表述为 (x, y, 1) 变形推导为 (x + dx, y+ dy, 1)
此时线性变换便可作为工具描述变换过程了，引入变换矩阵后，该问题就变成了求解变换矩阵
已知:
Copy ( a b c d e f g h i ) ( x y 1 ) = ( x + d x y + d y 1 ) \begin{pmatrix}
a & b & c \\
d & e & f \\
g & h & i
\end{pmatrix}
\begin{pmatrix}
x \\
y \\
1
\end{pmatrix}
=
\begin{pmatrix}
x + dx \\
y+ dy \\
1
\end{pmatrix} a d g b e h c f i x y 1 = x + d x y + d y 1 得
Copy { a x + b y + c = x + d x d x + e y + f = y + d y g x + h y + i = 1 \begin{cases}
ax + by + c = x + dx \\
dx + ey + f = y + dy \\
gx + hy + i = 1
\end{cases} ⎩ ⎨ ⎧ a x + b y + c = x + d x d x + ey + f = y + d y gx + h y + i = 1 解得变换矩阵为
Copy ( 1 0 d x 0 1 d y 0 0 1 ) \begin{pmatrix}
1 & 0 & dx \\
0 & 1 & dy \\
0 & 0 & 1
\end{pmatrix} 1 0 0 0 1 0 d x d y 1 于是在数学层面我们就可以用这个变换矩阵来描述平移过程了。
2. 缩放#
描述从点 (x, y) 到 (sx*x, sy*y)，sx 与 sy 为常量。
引入齐次坐标，可表述为 (x, y, 1) 变形推导为 (sx*x, sy*y, 1)
引入变换矩阵
已知:
Copy ( a b c d e f g h i ) ( x y 1 ) = ( s x ∗ x s y ∗ y 1 ) \begin{pmatrix}
a & b & c \\
d & e & f \\
g & h & i
\end{pmatrix}
\begin{pmatrix}
x \\
y \\
1
\end{pmatrix}
=
\begin{pmatrix}
sx * x \\
sy * y \\
1
\end{pmatrix} a d g b e h c f i x y 1 = s x ∗ x sy ∗ y 1 得
Copy { a x + b y + c = s x ∗ x d x + e y + f = s y ∗ y g x + h y + i = 1 \begin{cases}
ax + by + c = sx * x \\
dx + ey + f = sy * y \\
gx + hy + i = 1
\end{cases} ⎩ ⎨ ⎧ a x + b y + c = s x ∗ x d x + ey + f = sy ∗ y gx + h y + i = 1 解得变换矩阵为
Copy ( s x 0 0 0 s y 0 0 0 1 ) \begin{pmatrix}
sx & 0 & 0 \\
0 & sy & 0 \\
0 & 0 & 1
\end{pmatrix} s x 0 0 0 sy 0 0 0 1 3. 旋转#
解释旋转需要引入单位圆。
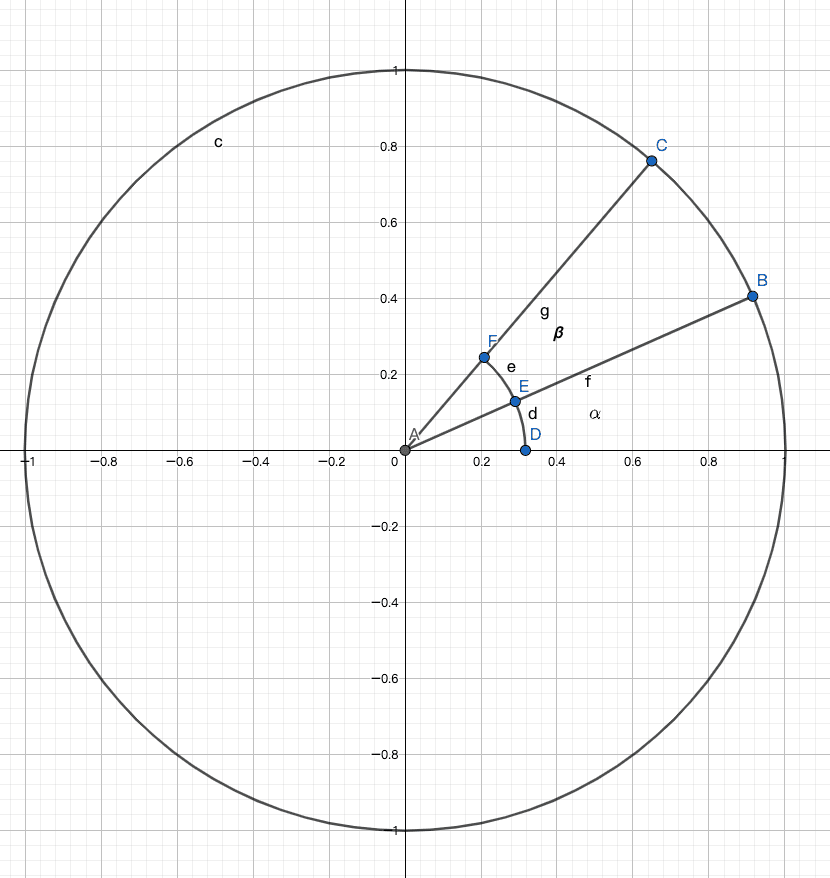
如图，点 B 旋转至 点 C 处，AB 与 X 轴的夹角为 α，AC 与 AB 夹角为 β
则 B 点坐标可表示为 (cosα, sinα), C 点坐标为 (cos (α + β), sin (α + β))
将 C 点坐标展开，则 C 点为 (cosα cosβ - sinα sinβ, sinα cosβ + cosα sinβ)
记 B 点坐标为 (x, y), C 点坐标则为 (x cosβ - y sinβ, y cosβ + x sinβ)
引入齐次坐标，可表述为 (x, y, 1) 变形推导为 (x cosβ - y sinβ, y cosβ + x sinβ, 1)
引入变换矩阵
已知:
Copy ( a b c d e f g h i ) ( x y 1 ) = ( x c o s β − y s i n β y c o s β + x s i n β 1 ) \begin{pmatrix}
a & b & c \\
d & e & f \\
g & h & i
\end{pmatrix}
\begin{pmatrix}
x \\
y \\
1
\end{pmatrix}
=
\begin{pmatrix}
xcosβ - ysinβ \\
ycosβ + xsinβ \\
1
\end{pmatrix} a d g b e h c f i x y 1 = x cos β − ys in β ycos β + x s in β 1 得
Copy { a x + b y + c = x c o s β − y s i n β d x + e y + f = y c o s β + x s i n β g x + h y + i = 1 \begin{cases}
ax + by + c = xcosβ - ysinβ \\
dx + ey + f = ycosβ + xsinβ \\
gx + hy + i = 1
\end{cases} ⎩ ⎨ ⎧ a x + b y + c = x cos β − ys in β d x + ey + f = ycos β + x s in β gx + h y + i = 1 解得变换矩阵为
Copy ( c o s β − s i n β 0 s i n β c o s β 0 0 0 1 ) \begin{pmatrix}
cosβ & -sinβ & 0 \\
sinβ & cosβ & 0 \\
0 & 0 & 1
\end{pmatrix} cos β s in β 0 − s in β cos β 0 0 0 1 4. 反射#
在数学中，反射是把一个物体变换成它的镜像的映射。要反射一个平面图形，需要 “镜子” 是一条直线（反射轴），对于三维空间中的反射就要使用平面作为镜子。
如果根据引用，那么反射可分为根据 X 轴反射与根据 Y 轴反射，但实际上也存在中心反射（点反射）这一概念
根据 X 轴反射#
描述点 (x, y) 到点 (x, -y)
已知:
Copy ( a b c d e f g h i ) ( x y 1 ) = ( x − y 1 ) \begin{pmatrix}
a & b & c \\
d & e & f \\
g & h & i
\end{pmatrix}
\begin{pmatrix}
x \\
y \\
1
\end{pmatrix}
=
\begin{pmatrix}
x \\
-y \\
1
\end{pmatrix} a d g b e h c f i x y 1 = x − y 1 得:
Copy { a x + b y + c = x d x + e y + f = − y g x + h y + i = 1 \begin{cases}
ax + by + c = x \\
dx + ey + f = -y \\
gx + hy + i = 1
\end{cases} ⎩ ⎨ ⎧ a x + b y + c = x d x + ey + f = − y gx + h y + i = 1 解得变换矩阵:
Copy ( 1 0 0 0 − 1 0 0 0 1 ) \begin{pmatrix}
1 & 0 & 0 \\
0 & -1 & 0 \\
0 & 0 & 1
\end{pmatrix} 1 0 0 0 − 1 0 0 0 1 根据 Y 轴反射#
描述点 (x, y) 到点 (-x, y)
已知:
Copy ( a b c d e f g h i ) ( x y 1 ) = ( − x y 1 ) \begin{pmatrix}
a & b & c \\
d & e & f \\
g & h & i
\end{pmatrix}
\begin{pmatrix}
x \\
y \\
1
\end{pmatrix}
=
\begin{pmatrix}
-x \\
y \\
1
\end{pmatrix} a d g b e h c f i x y 1 = − x y 1 得:
Copy { a x + b y + c = − x d x + e y + f = y g x + h y + i = 1 \begin{cases}
ax + by + c = -x \\
dx + ey + f = y \\
gx + hy + i = 1
\end{cases} ⎩ ⎨ ⎧ a x + b y + c = − x d x + ey + f = y gx + h y + i = 1 解得变换矩阵:
Copy ( − 1 0 0 0 1 0 0 0 1 ) \begin{pmatrix}
-1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{pmatrix} − 1 0 0 0 1 0 0 0 1 根据 点 (p, q) 反射#
描述点 (x, y) 到点 (2p-x, 2q-y)
已知:
Copy ( a b c d e f g h i ) ( x y 1 ) = ( 2 p − x 2 q − y 1 ) \begin{pmatrix}
a & b & c \\
d & e & f \\
g & h & i
\end{pmatrix}
\begin{pmatrix}
x \\
y \\
1
\end{pmatrix}
=
\begin{pmatrix}
2p-x \\
2q-y \\
1
\end{pmatrix} a d g b e h c f i x y 1 = 2 p − x 2 q − y 1 得:
Copy { a x + b y + c = 2 p − x d x + e y + f = 2 q − y g x + h y + i = 1 \begin{cases}
ax + by + c = 2p-x \\
dx + ey + f = 2q-y \\
gx + hy + i = 1
\end{cases} ⎩ ⎨ ⎧ a x + b y + c = 2 p − x d x + ey + f = 2 q − y gx + h y + i = 1 解得变换矩阵:
Copy ( − 1 0 2 p 0 − 1 2 q 0 0 1 ) \begin{pmatrix}
-1 & 0 & 2p \\
0 & -1 & 2q \\
0 & 0 & 1
\end{pmatrix} − 1 0 0 0 − 1 0 2 p 2 q 1 5. 错切#
定义见图，其实就像是图形在某一方向上的扭曲，底下只贴推导过程。需注意的是 α 与 β 范围为 [0, 90°)
y 轴为依赖轴的错切变换#
描述点 (x, y) 到点 (x + y.tanα, y)
已知:
Copy ( a b c d e f g h i ) ( x y 1 ) = ( x + y . t a n α y 1 ) \begin{pmatrix}
a & b & c \\
d & e & f \\
g & h & i
\end{pmatrix}
\begin{pmatrix}
x \\
y \\
1
\end{pmatrix}
=
\begin{pmatrix}
x+y.tanα \\
y \\
1
\end{pmatrix} a d g b e h c f i x y 1 = x + y . t an α y 1 得:
Copy { a x + b y + c = x + y . t a n α d x + e y + f = y g x + h y + i = 1 \begin{cases}
ax + by + c = x+y.tanα \\
dx + ey + f = y \\
gx + hy + i = 1
\end{cases} ⎩ ⎨ ⎧ a x + b y + c = x + y . t an α d x + ey + f = y gx + h y + i = 1 解得变换矩阵:
Copy ( 1 t a n α 0 0 1 0 0 0 1 ) \begin{pmatrix}
1 & tanα & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{pmatrix} 1 0 0 t an α 1 0 0 0 1 x 轴为依赖轴的错切变换#
描述点 (x, y) 到点 (x, y + x.tanβ)
已知:
Copy ( a b c d e f g h i ) ( x y 1 ) = ( x y + x . t a n β 1 ) \begin{pmatrix}
a & b & c \\
d & e & f \\
g & h & i
\end{pmatrix}
\begin{pmatrix}
x \\
y \\
1
\end{pmatrix}
=
\begin{pmatrix}
x \\
y + x.tanβ \\
1
\end{pmatrix} a d g b e h c f i x y 1 = x y + x . t an β 1 得:
Copy { a x + b y + c = x d x + e y + f = y + x . t a n β g x + h y + i = 1 \begin{cases}
ax + by + c = x \\
dx + ey + f = y + x.tanβ \\
gx + hy + i = 1
\end{cases} ⎩ ⎨ ⎧ a x + b y + c = x d x + ey + f = y + x . t an β gx + h y + i = 1 解得变换矩阵:
Copy ( 1 0 0 t a n β 1 0 0 0 1 ) \begin{pmatrix}
1 & 0 & 0 \\
tanβ & 1 & 0 \\
0 & 0 & 1
\end{pmatrix} 1 t an β 0 0 1 0 0 0 1 
